Ohm’s law, power triangle, and common electrical formulas on a notepad

Math & Formulas You Actually Use

Ohm’s Law, power, kVA↔amps, voltage drop, motors, transformers, and quick constants—clean, exam-focused math.

10
Major Articles
15
Quiz Questions
20
Visual Examples
🧮

Ohm’s Law & Real Power Relationships

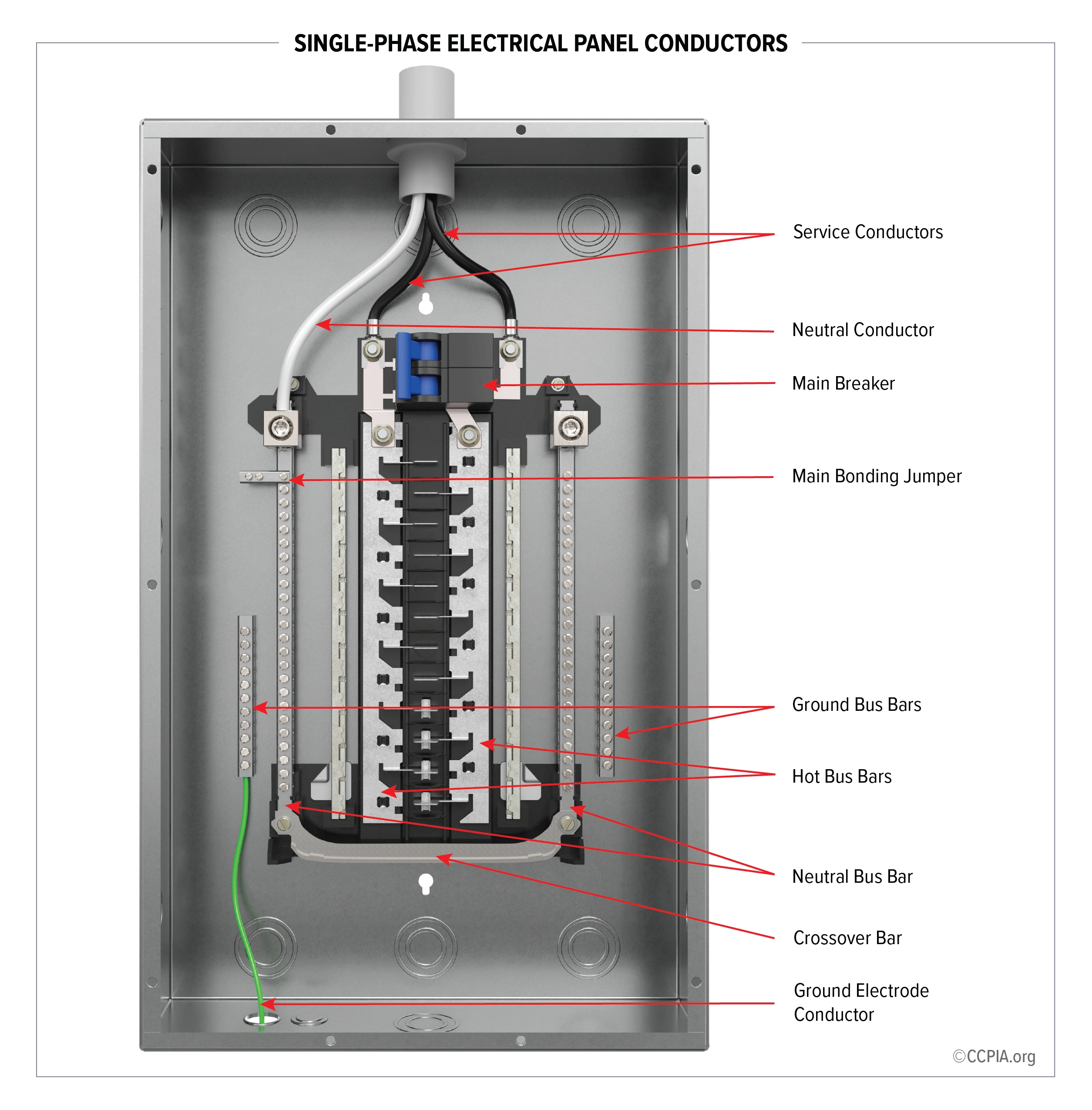
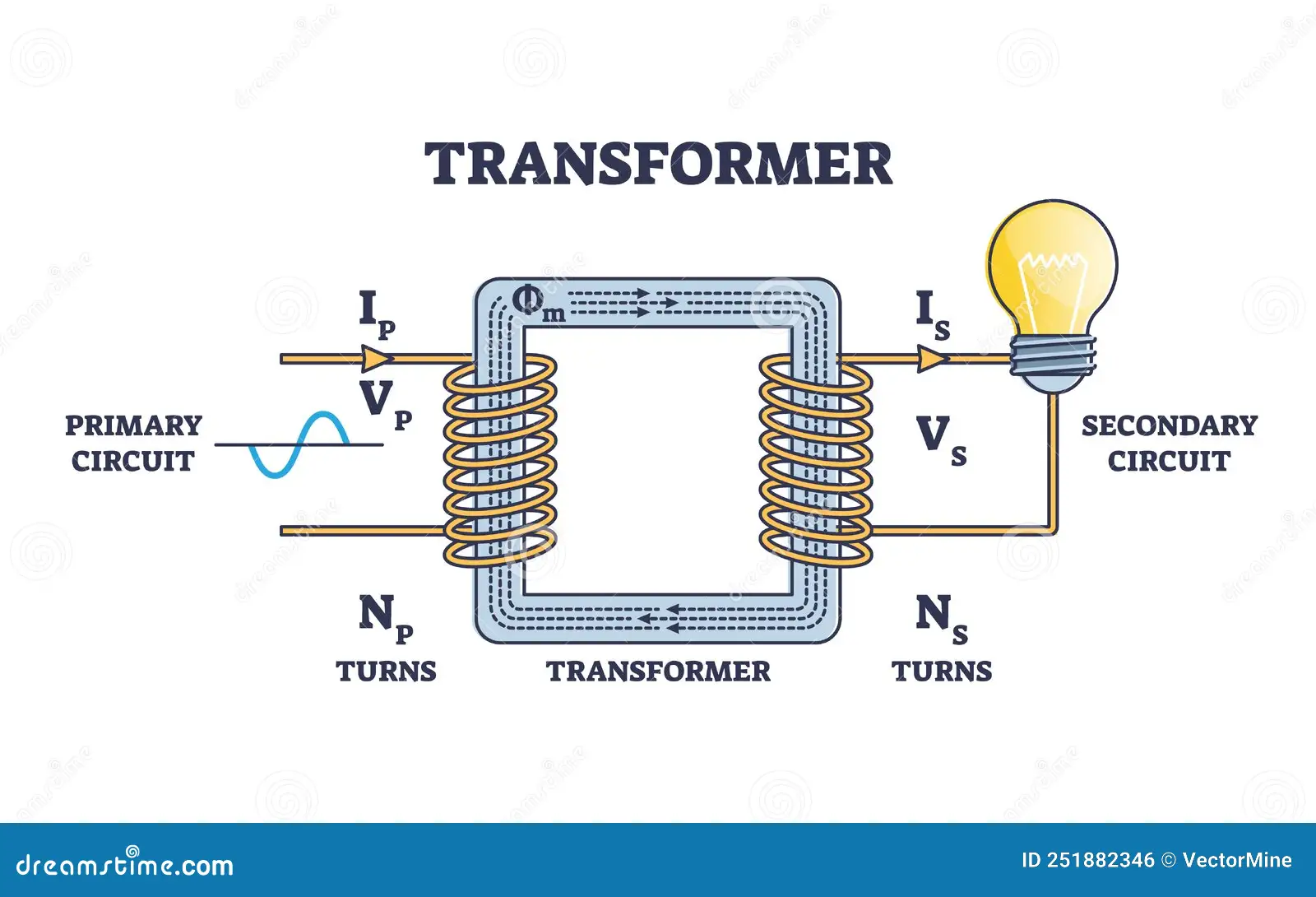
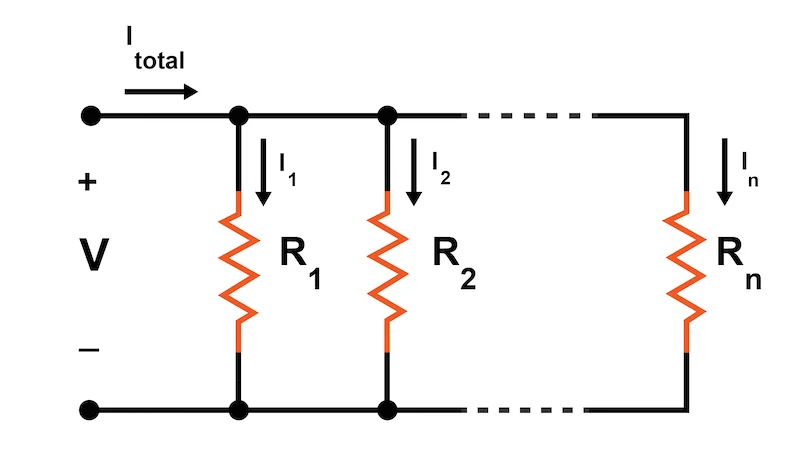
  • OhmV = I × R; I = V ÷ R; R = V ÷ I. Memorize the triangle; exams mix algebra steps.
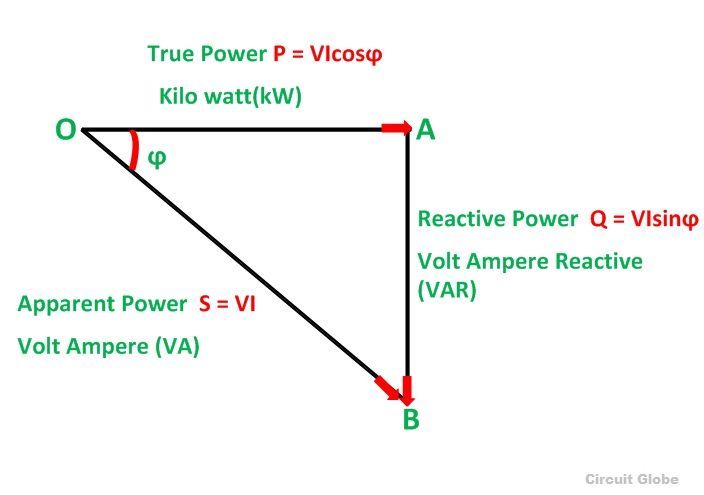
  • PowerP = V × I (W). With power factor: P(kW) = V × I × PF ÷ 1000 (1ϕ), or × √3 for 3ϕ.
  • kVAS(kVA) = V × I ÷ 1000 (1ϕ), or V × I × √3 ÷ 1000 (3ϕ). kW = kVA × PF.
  • EnergykWh = kW × hours. Utility billing ties to energy, not just power.
RULE OF THUMB
One Triangle, Many Answers
For exam speed: remember the V–I–R and P–V–I triangles. Derive the rest.
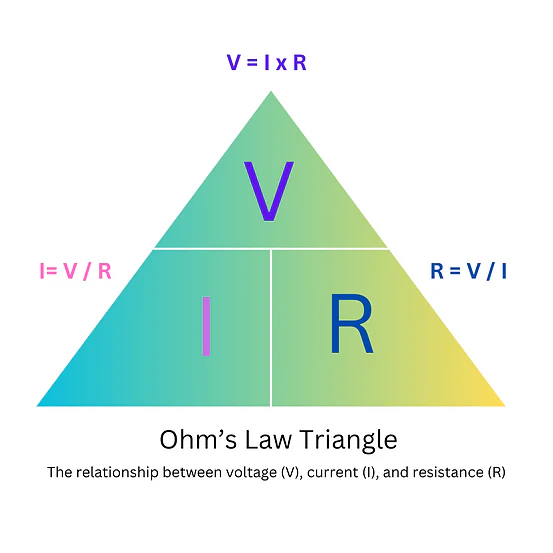
Ohm’s law triangle on paper
Cover one variable to get the formula.
Power equations on whiteboard
kW, kVA, PF—know how they relate.
🔌

Single-Phase vs Three-Phase Power

  • 1ϕkW = V × I × PF ÷ 1000. kVA = V × I ÷ 1000.
  • 3ϕkW = √3 × V(line-line) × I × PF ÷ 1000. kVA = √3 × V × I ÷ 1000.
  • Exam CueIf you see 3ϕ and LL voltage, multiply by √3. If given LN, convert or confirm what current references.
EXAM TRAP
Watch the √3
Most misses come from forgetting √3 on 3ϕ or using LN values in LL formulas.
Three-phase phasor diagram
√3 shows up in 3ϕ line values.
Single-phase panel
1ϕ math is simpler—no √3 factor.
📋

kVA ↔ Amps Quick Table

  • UseFast lookups during sizing. Always state assumptions (1ϕ vs 3ϕ).
  • PFkVA ignores PF; use kW relation if PF is given/required.
TABLE
Common Voltages — Approx Amps
SystemS (kVA)Approx I (A)
1ϕ 120V10≈ 83
1ϕ 240V10≈ 42
3ϕ 208V30≈ 83
3ϕ 240V30≈ 72
3ϕ 480V75≈ 90
3ϕ 480V150≈ 180
Formulas: 1ϕ I ≈ (kVA×1000)/V; 3ϕ I ≈ (kVA×1000)/(√3×V). Round sensibly.
Printed quick table
Keep a tiny kVA→A card for interviews/exams.
MCC buckets
Tables help estimate feeder sizes quickly.
⚡

Voltage Drop — DC vs AC Workflow

  • DC/UnityUse Table 8 resistance (Ω/1000 ft). VD ≈ 2 × L × I × R (1ϕ 2-wire). Adjust path length correctly.
  • AC 3ϕUse Table 9 (R & X). VD% ≈ (100 × √3 × I × (R cosφ + X sinφ))/V. PF matters.
  • ExamState conductor metal, size, temp assumption if unspecified; pick correct table (8 or 9).
NEC REFERENCE
Pick Table 8 or 9 First
DC/Unity PF → Table 8. 3ϕ with PF → Table 9 (R & X). Then compute VD or allowable length.
Hand calc showing VD steps
Write your chosen table at the top.
Fluke meter VD reading
Field VD corroborates your calc.
🛠️

Motors — Nameplate vs Table, HP, and Current

  • 430 TableSizing generally uses 430 tables current—not the nameplate—unless the section says otherwise.
  • HP↔kW1 HP ≈ 746 W. Don't convert unless the problem requires it.
  • OCPD/ConductorConductor ampacity and OCPD % values vary by motor type; know 'typical' 125% conductor sizing pattern.
EXAM TRAP
Use 430 Tables for Current
When sizing, default to 430 tables, not nameplate, unless specifically directed.
Motor nameplate
Nameplate matters, but sizing often uses Code tables.
Motor starter
Article 430 is a top exam area.
🔁

Transformers — Primary & Secondary Current

  • kVA→II(1ϕ) = kVA×1000/V; I(3ϕ) = kVA×1000/(√3×V). Compute for both sides.
  • %ZPercent impedance affects fault current; lower %Z → higher available fault current.
  • ProtectionPair current calcs with OCPD/secondary rules in 240/450 for typical exam prompts.
RULE OF THUMB
Work Both Sides
Always compute primary and secondary currents; annotate which side each value belongs to.
Dry-type transformer
Label: kVA, V, %Z—use them all.
Transformer diagram
Map primary/secondary clearly in your work.
🧩

Series & Parallel Resistance — Fast Rules

  • SeriesR_total(series) = R1 + R2 + …
  • ParallelR_total(parallel) = 1 / (1/R1 + 1/R2 + …). Two equal resistors → R/2.
  • Exam CueWatch units and where the drop occurs—series share current; parallel share voltage.
CHART
Two-Resistor Parallel Example
R (Ω)100
Equivalent (Ω)50
Current ↑2
Two equal resistors in parallel halve the resistance and double current for a given voltage.
Parallel resistor diagram
Equal values make mental math easy.
Series resistor ladder
Series adds—simple check.
💥

Available Fault Current — Quick Estimate

  • Basic3ϕ bolted fault at xfmr: I_sc ≈ (kVA×1000) / (√3 × V × (%Z/100)).
  • DistanceDownstream conductors/impedance reduce current—estimate quickly with conductor data if provided.
  • LabelingTie result to SCCR labeling requirements (see Module 1 quick hits).
EXAM TRAP
Units & %Z
Convert %Z to a decimal in the denominator. Keep track of 3ϕ factor (√3).
Service gear with labels
Your calc informs labeling.
Transformer data plate
%Z drives the math.
📐

Power Factor & Basic Correction

  • TrianglekVA² = kW² + kVAR². PF = kW/kVA = cosφ.
  • CorrectionkVAR_needed ≈ kW × (tanφ₁ − tanφ₂). Often to raise PF to 0.9-0.95.
  • Exam CueIf no correction target is given, compute present PF from given kW/kVA.
NEC REFERENCE
Write the Triangle First
Sketch kW (adjacent), kVAR (opposite), kVA (hypotenuse). Then plug numbers.
Power triangle sketch
Visual solves half the problem.
Capacitor bank
Cap banks supply kVAR to improve PF.
📝

Constants & Rounding — Speed Pack

  • √3≈ 1.732
  • HP1 HP ≈ 746 W
  • kcmil1 kcmil = 1000 circular mils
  • RoundState rounding method; keep at least 2-3 sig figs unless Code/table dictates otherwise.
TABLE
Handy Constants & Conversions
ItemValue / Note
√3≈ 1.732
1 HP≈ 746 W
kW ↔ kVAkW = kVA × PF
Amps (3ϕ)I ≈ (kVA×1000)/(√3×V)
kWhkW × hours
Write constants at the top of your scratch page so you don’t second-guess mid-problem.
List of constants on a card
One card, all constants.
Scratch sheet with constants
Prevent mental stalls with a pre-list.

Math — Exam Quick Hits

Ohm’s Law

V = I×R. P = V×I. kW = kVA×PF.

1ϕ vs 3ϕ

3ϕ uses √3 with line-line voltage.

Voltage Drop

DC/Table 8; AC 3ϕ/Table 9 with PF.

Motors

Use Article 430 tables for sizing.

Transformers

Compute I on both sides.

Fault Calc

I_sc ∝ kVA/%Z (with √3).

Knowledge Check

Answer all questions, then click Submit Answers. You’ll see your score after submitting. Nothing is graded until then.

1

Ohm’s Law states:

2

Real power for single-phase with PF is:

3

Three-phase kVA is calculated by:

4

A 75 kVA, 480 V, 3ϕ load draws approximately:

5

For DC or unity-PF voltage drop you should use:

6

Three-phase voltage drop with PF generally uses:

7

When sizing motors for feeders and OCPD, the current usually comes from:

8

Transformer secondary current (3ϕ) is given by:

9

1 horsepower is approximately:

10

Two equal resistors in parallel have an equivalent resistance of:

11

Available fault current at the transformer secondary is roughly proportional to:

12

Power factor equals:

13

A 30 kVA, 240 V single-phase load draws approximately:

14

Which statement is TRUE about kW and kVA?

15

For 3-phase problems, forgetting this factor is a common exam error: